A vertically-Lagrangian, non-hydrostatic, multilayer model for multiscale free-surface flows
I will present a semi-discrete, multilayer set of equations describing the three-dimensional motion of an incompressible fluid bounded below by topography and above by a moving free-surface. This system is a consistent discretisation of the incompressible Euler equations, valid without assumptions on the slopes of the interfaces. Expressed as a set of conservation laws for each layer, the formulation has a clear physical interpretation and makes a seamlesslink between the hydrostatic Saint-Venant equations, dispersive Boussinesq-style models and the incompressible Euler equations. The associated numerical scheme, based on an approximate vertical projection and multigrid-accelerated column relaxations, provides accurate and efficient solutions for all regimes. The same model can thus be applied to study metre-scale waves, even beyond breaking, with results closely matching those obtained using small-scale Euler/Navier-Stokes models, and coastal or global scale dispersive waves, with an accuracy and efficiency comparable to extended Boussinesq wave models. The implementation is adaptive, parallel and open source as part of the Basilisk framework (basilisk.fr).
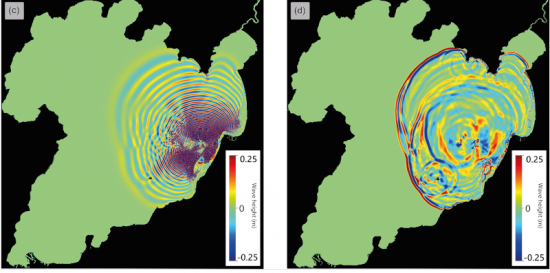
Figure : Multilayer model of the wave field generated by a volcanic eruption under [lake Taupo, New Zealand](https://en.wikipedia.org/wiki/Lake_Taup%C5%8D). Left : dispersive, right : non-dispersive. From [Hayward et al, 2022](http://basilisk.fr/Bibliography#hayward2022).
Contact Nathanael Machicoane for more information or to schedule a discussion with the seminar speaker.




