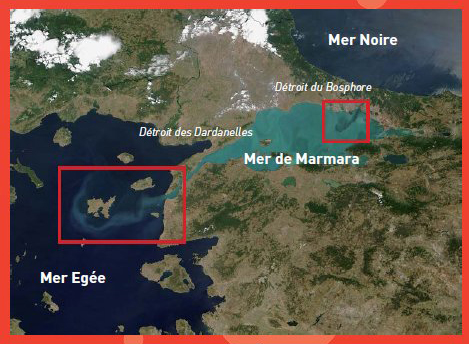
En 1835, un ingénieur et mathématicien français, Gaspard Coriolis, montre qu’un corps de masse M en mouvement V dans un système tournant ω, est soumis à un force Fc perpendiculaire à ce mouvement. Il lui a donné son nom :
Fc = 2Mω x V
En 1851, Léon Foucault installe un long pendule de 65 m au Panthéon. Il montre que les déviations observées à chaque période sont dues à la force de Coriolis. Il va ainsi mettre en évidence la rotation de la Terre.
Pour comprendre la force de Coriolis, imaginons un joueur de pétanque qui, à partir d’un point A, lance sa boule en l’air en direction du cochonnet B.
Observons alors ce qui se passe dans trois situations différentes :
Sans rotation :
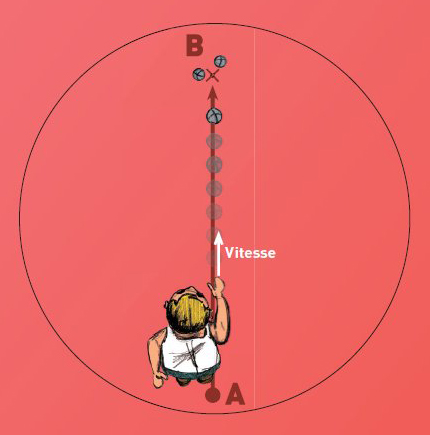
Avec rotation (hémisphère Nord) :
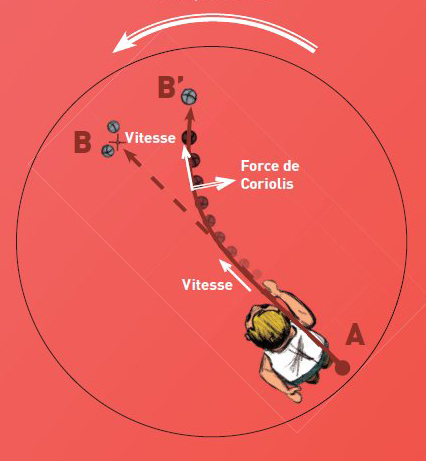
Avec rotation (hémisphère Sud) :
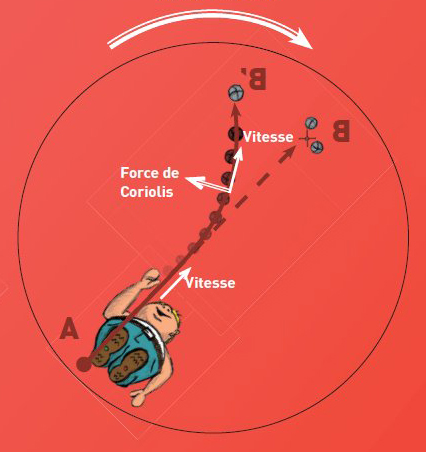
Dans l’océan et l’atmosphère
- A l’hémisphère Nord : la force de Coriolis est à droite de la vitesse
- A l’hémisphère Sud : la force de Coriolis est à gauche de la vitesse
- La force de Coriolis est donc nulle à l’équateur et maximum aux pôles
L’effet Coriolis est d’autant plus grand que :
- La vitesse de rotation est grande (grande déviation BB’)
- Le temps de parcours AB’ est grand (petites vitesses et/ou grandes dimensions)
C’est donc dans l’océan et aux grandes latitudes que cet effet sera le plus important.
Quelques exemples de la nature :