Gravity currents are abundant in the geophysical context. They can develop over short/long distances before reaching continental slopes. Most laboratory experiments considered gravity currents on horizontal or constant slope, smooth boundaries, using finite volume releases. Studies of the layer flow of constant supply gravity currents on slopes have focused on the equilbrium state of the current. This state is considered to be reached at a distance from the supply of about 10 times the initial depth of the current. The flow up to this equilibrium state and the dependency on initial conditions and slope angle, which includes spatially developing currents due to topography changes, has received so far only little attentions.
Focus of this research is on the spatial development due to rapid topography changes of a continuously supplied dense current. We considered well developed currents on a horizontal boundary, having a large interfacial Richardson number before reaching concave or linear slopes. The resulting down-slope current was found to have a completely different behavior. Three distinct development regions were identified characterized by strong variations of velocity, entrainment and bottom friction coefficient (Negretti Flor and Hopfinger JFM 2017).
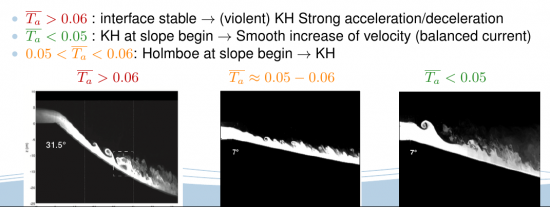

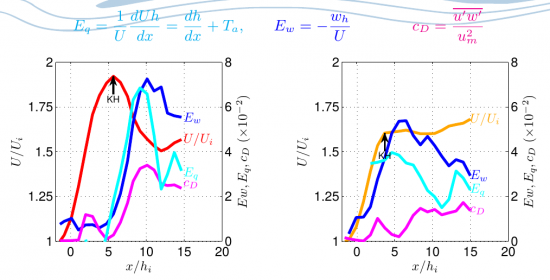
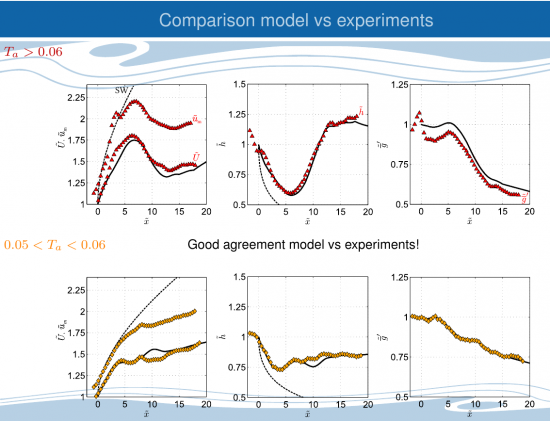
Based on these results, further experiments have been conducted to understand the influence of the initial conditions (Richardson number Ji) on the development of a steady-state gravity current over sloping boundaries. The initial development of the current before reaching the slope, expressed in terms of the initial Richardson number Ji, is crucial in determining its further development so that the current do not always reach the commonly assumed self-similar regime even within long distances.
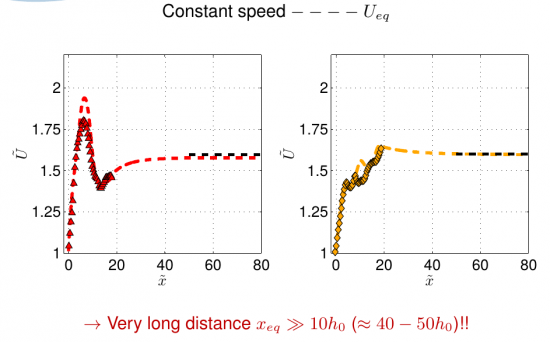
The drag terms (entrainment and bottom friction) cannot be predicted using the proposed relations available in the literature. The different reported current behaviours can be expressed in terms of an overall acceleration parameter which scales with the initial Richardson number Ji and the slope angle. By solving numerically the governing equations, the gravity flow velocity, depth and buoyant acceleration in the flow direction can be well predicted for all the performed experiments over the full measured domain. The numerical solution for the experiments with Ji>0.3 predicts that the current requires a distance 50 times larger than the current initial depth to reach an equilibrium state of constant velocity, which is much larger than the distance required in the case of a current with critical interface already at slope begin (Ji<0.3). These results are of interest since natural overflows may be far from this idealized condition and already well developed before reaching a descending topography (see in situ measurements in the Romanche fracture channel of van haren and Gostiaux 2014). Martin, Negretti and Hopfinger JFM 2019
We also considered a gravity current released from a lock into an ambient fluid of smaller density, that, from the beginning or after some horizontal propagation, propagates along an inclined (up- or down-) bottom. The flow (assumed in the inertial-buoyancy regime) has been modeled by the shallow-water (SW) equations with a jump condition applied at the nose (front). This work has been done in collaboration with Marius Ungarish at IIT Haifa, Israel. Results demonstrate that the accelerating-decelerating downstream current is reproduced well by a SW model combined with a simple closure for the entrainment and drag. A comparison of the theoretical results with previously published experimental data for both upslope flow and downslope flow show fair agreement. (Tamar Ungarish Martin and Negretti POF 2019).
The SW model has been also applied for a continuously supplied downslope gravity current head. (Martin Negretti and Ungarish 2019 (Phys Rev Fluids under review) )
Lock-release gravity currents flowing first on a horizontal and then up a slope have been investigated by means of theoretical analysis and laboratory experiments in collaboration with the University of Roma Tre (Italy) within the PhD of Maria Chiara De Falco who was visiting LEGI for 6 months in spring 2018. The slope angle θ ranged from 10° to 45°, and full- and partial-depth configurations were considered. The developed theoretical model, using the depth averaged momentum equation, provides new physical insight into the importance of the different driving forces and accounts for the
gravity component along the slope, whose effect increases with both the slope angle and the ratio of ambient fluid to current depth. The height of the current is assumed to decrease linearly with up slope distance and the spatial rate of decrease, expressed by the shape factor C, is determined from the theory, using the measured distance at which the current stops. This shape factor is found to depend on the slope only, in the form C’=0.4S where the slope S = tan θ. The front velocity is well predicted by the theory of all performed experiments indicating that the theory remains valid up to S ≈ 1, although some splashing occur already for S > 0.5.
De Falco, Adduce, Negretti and Hopfinger JFM 2019 (under review)
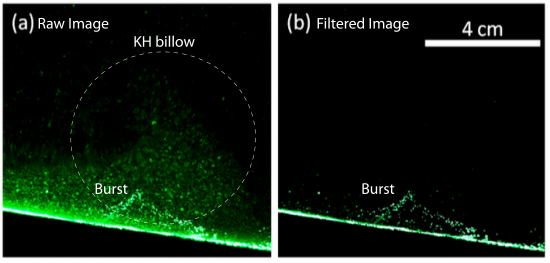
Further experiments have been performed over a sediment sloping boundary of continuously supplied gravity currents to investigate the effects of the observed high localized bottom friction on bed erosion. Also further experiments using a finite volume release gravity current over steep slopes and over a sediment bed have been performed recently at IRSTEA. Data are under processing.
Financement Labex Tec21 (Post-Doc Antoine Martin)
Collaborations : Marius Ungarish IIT Haifa,
Claudia Adduce, University Roma TRE Italy
PhD co-supervision Maria Chiara de Falco



