Travaux portés par Manuel Bernard et Guillaume Balarac.
Financement : PSPC INNOV’HYDRO, CNRS
Collaboration : G. Lartigue et V. Moureau (CORIA, Rouen)
L’objectif de ces travaux est d’améliorer la précision des calculs réalisés par méthode volumes finis sur maillages non-structurés. En effet, les erreurs de discretisation augmentent lorsque la qualité des maillages se dégrade, c’est à dire lorsque la forme des volumes de contrôle est de moins en moins régulière. Ainsi, l’utilisation de méthodes d’ordre élevé permet soit de réduire le niveau d’erreur pour un même maillage, soit d’utiliser un maillage plus grossier pour un niveau d’erreur fixé.
Cette méthode repose sur trois principes :
- Tout d’abord, étant donné que les grandeurs obtenues par méthode volumes finis sont constantes par volume de contrôle, il est nécessaire de les déconvoluer pour obtenir les valeurs nodales correspondantes.
- Une fois que les valeurs nodales d’une quantité et de ses dériviées successives sont connues avec suffisament de précision, il est possible de réaliser des développements en série de Taylor en tout point du domaine.
- Enfin, les flux sont intégrés de façon précise sur chacune des faces des volumes de contrôle.
Un des avantages de cette méthode par rapport à d’autres méthodes d’ordre élevé réside dans le fait que, jusqu’à une implémentation d’ordre 3, le stencil reste compact (seuls les voisins directs sont utilisés). Cette caractéristique est particulièrement intéressante dans un contexte de calcul haute performance puisqu’il assure un bon comportement des calculs parallélisés par méthode de décomposition de domaine.
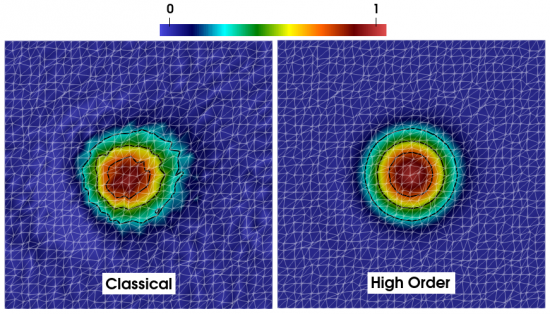
Les applications de cette méthode sont multiples, par exemple : interpolation entre maillages, calcul de courbure pour les méthodes Level-Set, intégration des flux convectifs et diffusifs. La figure représente la distribution spatiale d’une tâche scalaire après avoir été transportée durant une période (un tour de domaine périodique) par un champ de vitesse uniforme et constant. On observe qu’avec les méthodes d’ordre élevé développées dans cette étude, le signal est transporté plus fidèlement : les iso-contours sont réguliers et le scalaire borné entre 0 et 1.
Cette méthodologie a ensuite été étendue à la résolution des équations de Navier-Stokes pour des fluides incompressibles. Une première implémentation, entièrement d’ordre 3 a d’abord été testée et validée avec des résultats satisfaisants pour plusieurs configurations d’écoulements laminaires, par exemple pour un écoulement de canal de Poiseuille ou un écoulement de rhéomètre de Couette. Cependant, les simulations de configurations fortement turbulentes se sont révélées instables. Une inplémentation hybride en 2ème et 3ème ordre a quant à elle permis d’obtenir des simulations stables et offrant un gain de précision significatif par rapport aux schémas classiques.
Nous présentons ici les résultats obtenus pour un écoulement turbulent dans une conduite. L’évaluation de la précision des schémas numériques est moins directe pour les écoulements turbulents que pour les écoulements laminaires, car la solution des équations de Navier-Stokes ne converge pas, par définition, vers une solution analytique stationnaire. En revanche, elle converge vers un état statistique stationnaire où différentes quantités sont connues, soit par l’expérience, soit par des simulations numériques directes (DNS). Par la suite, nous ne considérerons que le champ de vitesse moyen arithmétique en temps, noté UMOYEN, et le champ de vitesse quadratique moyen en temps, noté URMS. Afin de maintenir un nombre raisonnable de nœuds de calcul, nous utilisons la méthodologie de convergence automatique de maillage (AMC) proposée par [2]. Cette procédure repose sur un critère de qualité QC1, introduit par [1], qui décrit la précision d’une solution discrète donnée. Dans la partie suivante, nous utilisons la formulation adimensionnelle proposée par [4]. Pour évaluer l’amélioration de la précision de la solution avec notre nouveau schéma par rapport au schéma classique de volumes finis utilisé précédemment, nous étudions un écoulement turbulent en conduite à Re = 3300, en utilisant les résultats d’une DNS sur un maillage régulier axisymétrique comme solution de référence [3].
La figure ci-dessous montre la norme L2 de l’erreur sur les champs UMOYEN et URMS. Le nouveau schéma permet une description légèrement meilleure du champ de vitesse moyen, en particulier sur les maillages grossiers (valeurs élevées de QC1adim). L’amélioration est encore plus marquée pour le champ de vitesse URMS, l’erreur étant réduite de 20 % à 50 % avec le nouveau schéma par rapport à l’ancien. Les travaux en cours portent sur l’amélioration de la stabilité et de la robustesse des simulations tout en utilisant des termes d’ordre supérieur dans les développements de Taylor et les intégrations de surface. En effet, le cadre haute-précision actuel est initialement conçu pour l’ordre 3, alors que les développements présentés dans ce rapport restent à l’ordre 2. Cependant, les premiers résultats obtenus avec une version simplifiée de la méthodologie restent très prometteurs, que ce soit en termes de réduction de l’erreur pour une taille de maillage donnée, ou de réduction du coût de calcul pour un niveau d’erreur donné.
[1] P. Benard, G. Balarac, V. Moureau, C. Dobrzynski, G. Lartigue, and Y. D’Angelo. Mesh adaptation for large-eddy simulations in complex geometries. International Journal for Numerical Methods in Fluids, 2015.
[2] A. Grenouilloux, J. Leparoux, V. Moureau, G. Balarac, T. Berthelon, R. Mercier, M. Bernard, P. Bénard, G. Lartigue, and O. Métais. Toward the use of LES for industrial complex geometries. Part I : automatic mesh definition. Journal of Turbulence, 24(6-7) :280–310, 2023.
[3] J. Kim, P. Moin, and R. Moser. Turbulence statistics in fully developed channel flow at low Reynolds number. Journal of fluid mechanics, 177 :133–166, 1987.
[4] H. Lam, T. Berthelon, G. Balarac. Non-dimensional meshing criterion of mean flow field discretization for rans and les. Computers & Fluids. 291. 106572, 2025.
Publications
Peer-reviewed Publications
2023
2021
2020