Title : Dynamics of a fluid particle in isotropic turbulence : scaling laws and stochastic modeling
Contact : Nathanael Machicoane
Abstract : Fluid-particle acceleration is intimately related to the dissipation rate of turbulence, in line with the Kolmogorov assumptions. On the other hand, various experimental and numerical works have reported as well its dependence on the kinetic energy. In this talk, we discuss the statistics of the fluid-particle acceleration conditioned on both the local dissipation rate and the kinetic energy. We show that this quantity presents an exponential dependence on the kinetic energy, in addition to the expected power law behavior with the dissipation rate. The exponential growth, which clearly departs from the previous propositions, reflects the additive nature of the kinetic energy, and gives the possibility to see the acceleration as a multiplicative cascade process integrating the effects of sweeps by the flow structures of all size. It is further proposed scaling laws for the Reynolds number dependence of the conditional and unconditional acceleration variance using Barenblatt’s incomplete similarity framework.
On the basis of these observations, we propose a stochastic model for the dynamics of a tracer in turbulent flows. Using a multiplicative model for the dissipation rate recently proposed, as well as an additional hypothesis on the structure of the diffusion tensor ("maximum winding hypothesis"), we will show that this model presents the essential characteristics of the "Lagrangian turbulence" highlighted in recent years, namely (i) non-Gaussian PDF of acceleration, (ii) scale separation between the norms of the acceleration and its components, (iii) anomalous scaling law for the Lagrangian velocity spectra, and (iv) negative skewness of the power increments, reflecting the temporal irreversibility, and is in good agreement with direct numerical simulations.
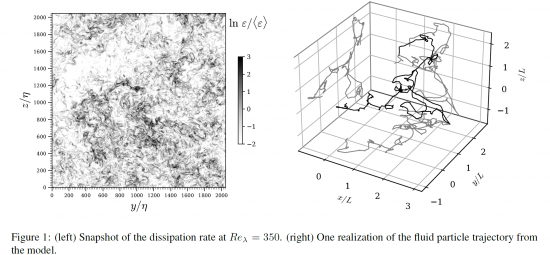
NB : We will take time to introduce the aspects related to multiplicative cascades and stochastic modeling.
More details : https://hal.archives-ouvertes.fr/hal-03408311/




